1 简单
交互式证明,又名交互式博弈,已经成为 Optimistic Rollups 仲裁机制的事实标准。通过使用中间指令为链上和链下提供统一的确定性单步执行环境,最大限度地减少链上仲裁期间的资源需求。它固有的复杂性导致我们为了传播和理解而简化其解释。让我们先看看它可以描述的多简单1。
1.1 同一语言,同一结果
Moe:Uno mas uno es igual a dos 在你的电脑上也成立吗?
Joe:我不懂西班牙语,你什么意思?你能用大家都能理解的数学语言描述一下吗?
Moe:1 + 1 = 2 在你的电脑上也如此吗?
Joe:Yes!
Moe:1 + 1 = 2 在每个人的计算机上都成立吗?
Everyone:Yes!
Moe:(((1 + 1) + 1) + 1) = 4 在每个人的计算机上也成立吗?
每个人:Yes!
1.2 同一语言与步骤,两种结果
Moe:(((1 + 1) + 1) + 1) = 5 在你的电脑上也成立吗?
Joe:不!它是 4。
Moe:我觉得 5 是对的。我们邀请尊敬的学者洛伦兹先生2来裁决,怎么样?
Joe:太好了。但洛伦兹先生相当的忙,我们可以先自行找到第一个不一致的步骤,然后请求他验证这个步骤。
Moe:这行得通吗?
Joe:可以。每一步都是确定性的。
Moe:让我们从第一步求值开始吧!
Joe:Okay!
……
Moe & Joe:在第 2 步中,我们得到了不同的结果。Moe 是 2 + 1 = 4,Joe 是 2 +1 = 3。我们来寻求他的帮助吧!
Lorentz:2 + 1 = 3
Moe & Joe:谢谢!
1.3 同一语言与步骤,两种结果,LogN 次核对
Moe:(((1 + 1) + 1) + ... + 1) = 48784359345934 在你的电脑上也成立吗?
Joe:不。它的值是 48784359345935。
Moe:我们再玩一次游戏吧!
Joe:决不!由于通信开销,每次比较需要 1 秒。我们可能需要 150 万年才能完成比较。
Moe:总共的计算成本仅为 1 秒。使用二分法怎么样?
Joe:每次比较都可以解决一半的问题。通过这种方式,我们可以快速识别不一致的地方!
Moe:第 24392179672966 步是 24392179672966 + 1 = 24392179672967
Joe:第 24392179672966 步是 24392179672965 + 1 = 24392179672966
Moe:第 12196089836483 步是 12196089836483 + 1 = 12196089836484
Joe:第 12196089836483 步是 12196089836482 + 1 = 12196089836483
Moe:第 6098044918241 步是 6098044918241 + 1 = 6098044918242
Joe:第 6098044918241 步是 6098044918241 + 1 = 6098044918242。第一个不一致的步骤一定在 (6098044918241, 12196089836483],我们离目标不远了!
2 深入
在“简单”中,我们确定了构成“交互式博弈”的三个基本要素:
a. 同一语言
b. 确定性步骤
c. 二分法
人们不禁会想,这么一个简单的协议是如何让众多的 Optimistic Rollups 团队花费如此多的时间和精力的呢?这就像莱特兄弟发明飞机之前的时代一样,当时人们已经知道从 A 点到 B 点最快的方法不是翻山越岭,而是直线飞行。飞行的动作就像二分法一样简单明了。为了吸引那些以前开车改坐飞机的人,强调这一点就足够了。然而,对于一名飞机工程师来说,显然还有更多东西需要了解。
2.1 同一语言
Moe:我们需要一种支持区块链客户端操作并与链上一致的语言。
Joe:搞定!对于以太坊来说,就是 Solidity!
Moe:您打算如何处理这些依赖于时空的指令?如:CALLER、SLOAD、SSTORE、BLOCKTIME。
Joe:嗯……我现在不能告诉你,但总有办法的,不是吗?
Moe:Optimism 曾尝试过这一点,但失败了。
Joe:可惜。感谢他们的贡献。
Moe:我们可以模拟一种语言的执行容器。 EVM-in-EVM 怎么样?
Joe:听起来不错。但是 Gas 成本呢?我认为在 Solidity 中模拟内存和存储并不是一件容易的事。
Moe:我们需要一种媒介,就像我们利用数学语言那样。
Joe:我认为我们已经接近答案了。
Moe:客户端可以编译为这种语言。我们可以在链上模拟这种语言。
Joe:理想情况下,它应该是一种汇编语言,因为模拟指令的执行总是更简单。
2.2 确定性步骤
Moe:通过使用某种语言,我们可以大致实现计算的确定性。因此,现在要解决的问题是输入和状态变化的确定性。
Joe:一般来说,我们使用预言机来解决与外部信息输入相关的问题。
Moe:这个预言机对于 L1 和 L2 都具有确定性吗?
Joe:我们在 L1 上有根(哈希),这意味着我们有机会验证输入。
Moe:能否画一张图来描绘我们目前取得的结果?
Joe:当然!

Moe:能解释一下这个图表吗?
Joe:
预执行:通过
block_hash获取输入
加载模拟器:设置执行环境
验证输入:利用证据验证输入
状态转换:执行 L2 交易
Moe:听起来我们全都搞定了!
Joe:差不多。
2.3 二分法
Moe:作为最直接的部分,似乎没有什么值得讨论的。
Joe:我们需要确定证据的合法性。
Moe:签名还不够吗?
Joe:不够。有些人可能会选择装聋作哑。
Moe:明白了。L1 应在每一轮二分查找中验证证据。
Joe:是的。并且这样 L1 不仅可以得到不一致的 STEPi,还可以拿到二分后最后一条一致的 STEPi-1。
3 丑陋
在“深入”中,我们提炼出了构成“交互式博弈”的三个基本要素:
a. 同一语言:简单的汇编,可以在链下客户端运行并在链上进行模拟。
b. 确定性步骤:利用证据验证输入。
c. 二分法:在每一轮中验证证据。
到目前为止,交互式博弈是可爱的。然而,为了让它真正发挥作用,我们必须揭开它丑陋的一面。
3.1 同一语言:RISC
Moe:看来我们有很多选择,比如 MIPS、RISC-V,甚至 Wasm。
Joe:我们可以设计一个灵活的架构来支持各种语言。然而,在任何给定时刻只能使用一个。
Moe:哪一个是你的首选?
Joe:MIPS。但两年后将会是 RISC-V。
Moe:你这样说我更困惑了。
Joe:作为一个讲道理的人,让我来与你说道说道。首先,模拟 CPU 指令的抽象级别相当低。虽然它可能看起来很晦涩,但由于缺乏多层抽象,它实际上认知负担是比较轻的,因此我对 Wasm 并不是很热衷。
Moe:似乎有点道理。
Joe:在诸多 CPU 指令集中,RISC 无疑是一个更优越的选择,因为它的指令数量有限且稳定,并且规避了模拟复杂指令的困难。另外,加载-存储架构可以防止 ALU 操作中内存副作用的出现。需要特别注意的是,在我们的模拟器中内存状态变化的每一步都需要跟踪,因此实现寄存器-内存架构的困难可能只会导致无限的错误。考虑到编译器的成熟度和稳定性,我倾向于MIPS。
Moe:继续讲讲 RISC-V。
Joe:我们可以拥有 64 位地址空间,因为 MIPS 32 位提供的 4GB 内存空间有时会不够用。然而,无论使用什么指令集,我们都必须小心验证实现的正确性。
Moe:系统调用将如何实现?这很棘手。
Joe:我们可以巧妙地构建我们的程序来最大限度地减少系统调用的使用,部署我们自己的系统调用实现来替换通用的系统调用实现。我们的首要需求是保持链上链下状态变化的一致性,而不是创建一个通用模拟器。
Moe:当我提到系统调用时,我实际上的担忧是语言中的非确定性因素。系统调用代表模拟器与外部世界之间的一种交互形式,这种交互可能意味着非确定性。您提到了最小化和定制系统调用的方法,虽然不具体,但考虑到模拟器的所有方面都掌握在实现者手中,这确实是可行的。但我还是很担心,觉得还有很多不确定因素没有考虑到。
Joe:我理解你的担忧,你甚至已经开始考虑下一阶段的问题了。让我们首先假设我们已经拥有这样的媒介,并在下一节中继续讨论。
Moe:中间表达对于所有链都是无偏见的,这听上去潜力很大。
Joe:是的。我们可以在不同的链上实现它的模拟器,这样大家都有交互式博弈了。我听说过一个项目就是这样做的。
Moe:Rooch/flexEmu (opens in a new tab)
Joe:就是它了!
3.2 确定性步骤:过程,输入
Moe:搞快点,因为前面关于语言的部分还没有充分讨论。
Joe:确实,我们需要更深入地研究语言的确定性。
Moe:当我们讨论汇编语言的确定性时,实际上是在讨论指令的确定性。
Joe:指令由opcode和操作数构成。这正是确定性问题的两大来源:过程 和 输入 在指令层面的微观表现。关于 输入 在 “深入” 中我们有过初步讨论,待会再来详细分析。我们先需要确保指令副作用的唯一性
Moe:并发将是一个严重的问题。
Joe:是的。模拟器产生的输出(状态根)必须与生产环境中并行执行器计算的输出相同。
Moe:如何保证每一步并发执行的确定性?
Joe:Dr.Strange3 可以帮助我们。
Moe:你是认真的?
Joe:不,我是乔。我们不能这样做,我们的目的也不是建立这样一个系统。我们想要的仅是在模拟器之间获得相同的最终状态并保持相同的步骤状态。
Moe:哦,是的。达到同样的最终状态并不是一件难事。我们只需要……
Joe:排序器应该给每个交易一个序号。因果无关的 tx 可以并行执行,因果相关的严格依次执行。这样最终状态会与全局顺序执行一致。
Moe:现在我们可以放心的剔除并发对指令副作用的影响了。
Joe:除了并发交易之外,进程中还有很多并发执行单元。
Moe:最简单的方法是强制模拟器在单个线程上执行。
Joe:是的。
Moe:随机性是另一个不稳定因素。
Joe:让我们开始自下而上分析指令世界。
Moe:RISC 家族中没有直接支持随机操作的操作码。对于相关的系统调用,我们可以在模拟器中嵌入固定的随机数据源。这样,每个模拟器都可以在同一过程中获得一致的伪随机数。
Joe:搞定!
Moe:Linux 内核讨厌浮点数。模拟器也讨厌这个吗?
Joe:我们可以使用 SoftFloat 库,也可以直接禁止它。
Moe:听起来我们已经为确定性程序做好了一切准备。
Joe:还不够。不要忘记程序不能证明自己的清白。
Moe:L1 可以验证静态过程,只需要一个摘要。在交互式博弈开始之前,L1 合约将通过验证双方的内存状态来验证双方是否使用了一致的程序。
Joe:是的。这相当于一个可验证的boot过程。引导区的内存地址是固定的,双方仅需要提供一个简单的 merkle tree 证明即可。
Moe:你刚才提到,关于输入问题还有一些要补充的。
Joe:没错。我想再次强调一下可验证“验证 输入 过程“的重要性。链下对于 输入 的验证过程一定是可以被单步追踪的,这样 输入 的初始状态才能获得合法性。输入 作为内存状态的一部分,如果加载后的 输入 数据被有意篡改,都会导致状态树的证明无法给出,因为篡改意味着前序指令产生了副作用,但恶意节点在初始状态一致的情况下是无法给出副作用指令以证清白的
Moe:听上去有些绕口,但我能明白你的意思。核心是确保输入的确定性,那么加上过程的确定性,我们只能有确定性的单步状态了。无懈可击了。
Joe:我们还有“无意识的邪恶”的问题,这是一个很容易被忽视的问题。
Moe:作为你的分身,我知道你在说什么。实现确定性意味着我们在实现依赖物理介质的纯粹理性。单纯有了纯粹理性不能沾沾自喜,从而忘记了物理约束。
Joe:区块链网络是抗静默错误的,因为节点在验证过程中提供了充分的冗余。而单纯的区块链本身不具备这个性质,在异步验证的 L2 中,静默错误会导致诚实但出错的节点被惩罚。
Moe:静默错误的发生就像太阳东升西落一样必然。所以我们需要主动创造冗余,比如利用运行着不同架构的物理机共同计算同一个过程,汇总后作为当前节点的输出。类似的工作云服务商已经驾轻就熟了。
Joe:现在我们可以说我们已经有了确定性的步骤。
3.3 二分法:: 头等舱机票
Moe:二分法被谈论的最多,因为它是交互式博弈中的直接难题。但它现在看来,水到渠成了。
Joe:对,它是直接问题,因为它直接展现了交互现象,但答案是间接的。它依赖合适的中间语言媒介与确定性的语言执行实现。
Moe:这让我想起来了之前关于飞机的比喻。现在我们有飞机了,只需要买票了。
Joe:给我来张头等舱,谢谢!
附录 A:当模拟器在模拟时它在模拟什么
Joe:这次让我先开始吧。
Moe:来。
Moe:看看这段源码在你的机器上会变成什么样的指令:

Joe:你又抢先开口了。在我的 x86_64 上:

或:

Moe:因为我给你看了源代码。没空谈。在我的 RISC-V 上:
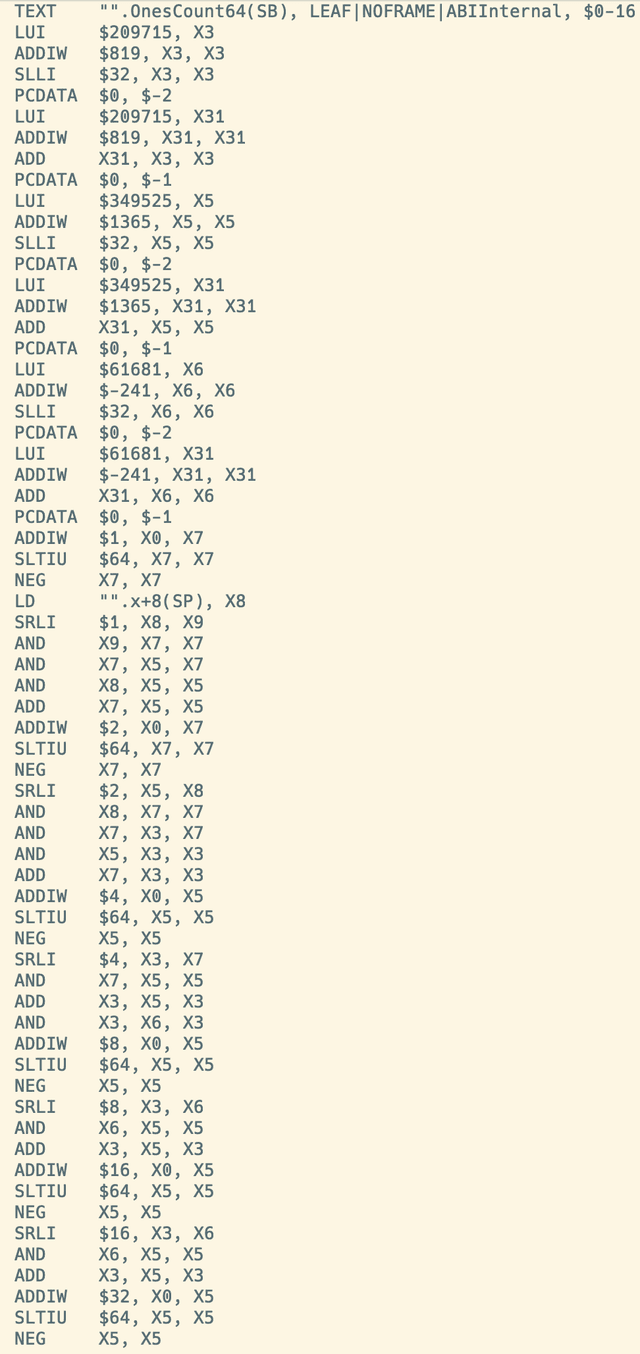
Joe:面对同样的输入,尽管我们的机器所运行的指令如此不同,它们还是能得到一样的输出。
Moe:是你在模拟我,还是我在模拟你?
Joe:这是一个问题。